########################Selection analyses############################# install.packages(c("car","reshape","ggplot2")) require(car) require(reshape) require(ggplot2) # Create data set dat <- data.frame(plant = seq(1,100,1), trait1 = rep(c(0.1,0.15,0.2,0.21,0.25,0.3,0.5,0.6,0.8,0.9,1,3,4,10,11,12,13,14,15,16), each = 5), trait2 = runif(100), fitness = rep(c(1,5,10,20,50), each = 20)) # Make relative fitness column dat_ <- cbind(dat, dat$fitness/mean(dat$fitness)) names(dat_)[5] <- "relfitness" # Standardize traits dat_ <- cbind(dat_[,-c(2:3)], rescaler(dat_[,c(2:3)],"sd")) ####Selection differentials and correlations among traits, cor.prob uses function in functions.R file ############################################################################ ####### Function for calculating correlation matrix, corrs below diagonal, ####### and P-values above diagonal ############################################################################ cor.prob <- function(X, dfr = nrow(X) - 2) { R <- cor(X) above <- row(R) < col(R) r2 <- R[above]^2 Fstat <- r2 * dfr / (1 - r2) R[above] <- 1 - pf(Fstat, 1, dfr) R } # Get selection differentials and correlations among traits in one data frame dat_seldiffs <- cov(dat_[,c(3:5)]) # calculates sel'n differentials using cov dat_selcorrs <- cor.prob(dat_[,c(3:5)]) # use P-values above diagonal for significance of sel'n differentials in dat_seldiffs dat_seldiffs_selcorrs <- data.frame(dat_seldiffs, dat_selcorrs) # combine the two ########################################################################## ####Selection gradients dat_selngrad <- lm(relfitness ~ trait1 * trait2, data = dat_) summary(dat_selngrad) # where "Estimate" is our sel'n gradient ####Check assumptions shapiro.test(dat_selngrad$residuals) # normality, bummer, non-normal hist(dat_selngrad$residuals) # plot residuals vif(dat_selngrad) # check variance inflation factors (need package car), everything looks fine plot(dat_selngrad) # cycle through diagnostic plots ############################################################################ # Plot data ggplot(dat_, aes(trait1, relfitness)) + geom_point() + geom_smooth(method = "lm") + labs(x="Trait 1",y="Relative fitness") ggsave("myplot.jpeg")
Plot of relative fitness vs. trait 1 standardized
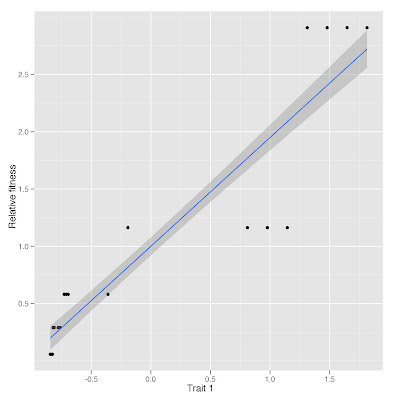
You can make the analysis in a simpler way:
ReplyDeletedat <- data.frame(plant = seq(1,100,1),
trait1 = rep(c(0.1,0.15,0.2,0.21,0.25,0.3,0.5,0.6,0.8,0.9,1,3,4,10,11,12,13,14,15,16), each = 5), trait2 = runif(100),
fitness = rep(c(1,5,10,20,50), each = 20))
#relativize fitness
dat$fitness.rel<-dat$fitness/mean(dat$fitness)
#standardize traits
dat$z.trait1<-scale(dat$trait1)
dat$z.trait2<-scale(dat$trait2)
#selection differentials are estimated commonly as cov(w,x), were w is relative fitness and x is #standardized trait value
#But in such conditions is exactly the same to estimate selection differentials using linear #regression, because regression slope equals cov(w,x)/var(x) and var(x)=1
#the advantage is to get P value in a single step
fit<-lm(fitness.rel ~ z.trait1, data=dat)
summary(fit)
Nice. I like the different approach to selection differentials. I will have to give that a try.
ReplyDeleteHi thanks for sharing thiis
ReplyDelete